勾股定理：悠悠4000年的故事

数学作为自然科学中最古老、最基础的学科之一，蕴藏着许多有趣的历史故事。而勾股定理，则是数学史上一颗璀璨的明珠，它不仅有着悠久的历史，更是数学中的基础定理之一。本文将带领读者一起探寻勾股定理这颗闪亮的数学明珠，揭开它悠悠4000年的故事。

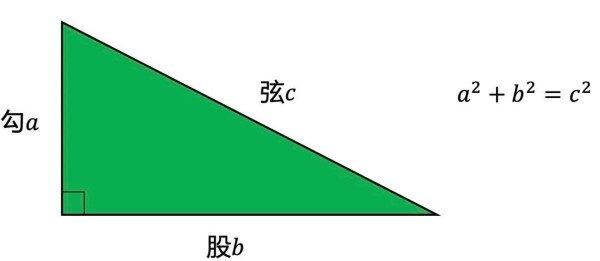
1. 勾股定理的起源

勾股定理最早可以追溯到古代的巴比伦、印度和中国。在巴比伦时期，人们已经发现了满足a^2 + b^2 = c^2的三元数组，这可以看做是勾股定理的雏形。在中国，《周髀算经》中就记载了勾股定理的特例。而在印度，早在公元前600年，数学家就已经研究勾股三元数组的性质。勾股定理在这些古代文明中的出现，展现了人类对几何关系的探索和认识，为后来的数学研究奠定了基础。此外，希腊数学家毕达哥拉斯也被广泛认为是勾股定理的发现者，他提出了一个三角形的定理，即：直角三角形的两条直角边平方和等于斜边平方。尽管毕达哥拉斯并没有给出证明，但是他的发现仍然为后人的研究提供了重要的启示。

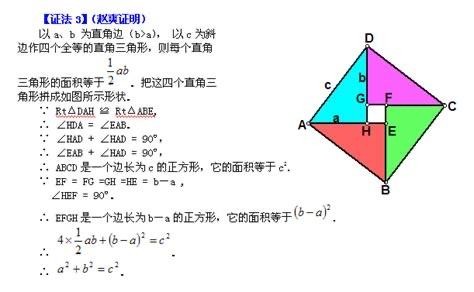
2. 勾股定理的完备证明

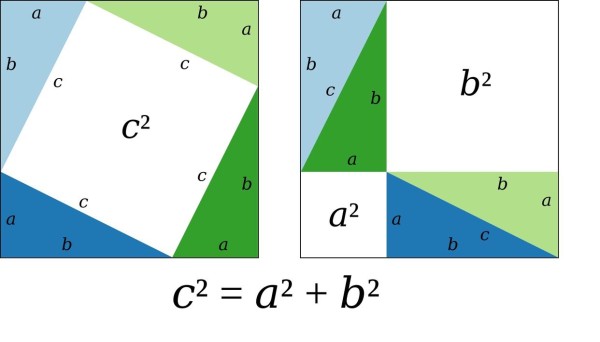
勾股定理最著名的证明方法要属毕达哥拉斯的证明了。他提供了一种几何证明，使得勾股定理得到了完备的解释和证明。随后，人们又发现了许多其他证明方法，包括代数证明、解析几何证明等，这都为勾股定理的深入理解提供了坚实的基础。例如，在近代数学中，欧几里得的《几何原本》中对勾股定理进行了系统的论述，并给出了不同于毕达哥拉斯证明的解析几何证明。同时，在17世纪，法国数学家费马提出了“费马大定理”，即勾股定理的一般化，但是直到300年后才被英国数学家安德鲁·怀尔斯和皮尔斯证明，这也被认为是数学史上的一个重要事件。

3. 勾股定理在现代的应用

今天，勾股定理已经成为数学中不可或缺的一部分，并在现代科学和工程中发挥着重要作用。从建筑设计到航天工程，从物理学到计算机科学，勾股定理都有着广泛的应用。例如，在建筑设计中，勾股定理被用于计算建筑结构的稳定性；在导航系统中，勾股定理被用于确定位置和航向；在物理学中，勾股定理被用于描述力学和电磁学等领域的问题。此外，勾股定理也是数学中的基础之一，它与三角函数、向量等概念密切相关，为人们更深入地理解这些概念提供了重要的基础。

结语

勾股定理是数学中一个古老而又充满活力的定理，它的历史悠久，应用广泛，对整个数学体系都具有深远的影响。通过了解勾股定理的起源和证明，我们可以更好地理解数学的发展历程，也可以更好地欣赏数学的美丽和神奇。希望通过本文的介绍，读者们能对勾股定理有更加深入的了解，也能对数学产生更大的兴趣和热爱。

网址：勾股定理：悠悠4000年的故事 http://c.mxgxt.com/news/view/794739

相关内容

婆媳关系的勾股定理
古韵悠悠，奔流不息（家在运河岸）
LOL十五周年爱情故事：她的卡莎，他的悠米
唐悠悠
再就业男团唱响光“音”故事，悠悠岁月中时间流淌，友情从未改变
吴悠
阿悠悠出场费,商演经纪人
阿悠悠
《lol》新英雄悠米背景故事 为寻找主人踏上旅途的猫
爱情公寓4唐悠悠资料

随便看看