概率论中的二项式定理与组合数学

发布时间：2024-12-26 23:39

　　在数学的广阔领域中，概率论和组合数学是两个紧密相连的分支。它们不仅在理论上相互影响，而且在实际应用中也发挥着至关重要的作用。本文将深入探讨概率论中的二项式定理及其在组合数学中的应用，以期帮助读者更好地理解这两个数学领域的内

　　一、二项式定理简介

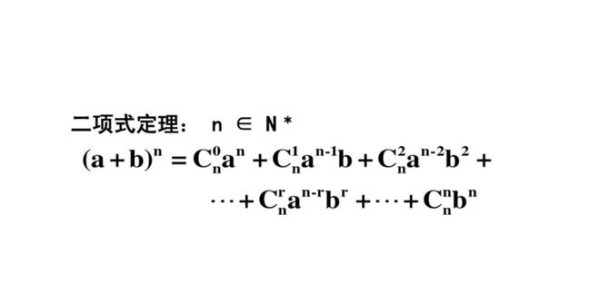
　　二项式定理是概率论中的一个基本定理，它描述了在有限次独立重复试验中，某个事件发生的概率。二项式定理的一般形式为：

　　$$(a+b)^n = \sum_{k=0}^{n} C_n^k a^{n-k} b^k$$

　　其中，$C_n^k$ 表示从n个不同元素中取出k个m.9znjcolz.com元素的组合数，也称为二项式系数。二项式定理在概率论中的应用主要体现在计算概率分布和求解概率问题。

　　二、二项式定理在概率论中的应用

　　计算概率分布

　　在概率论中，二项式定理可以用来计算二项分布的概率。二项分布是指在一定次数的独立重复试验中，某个事件发生的次数的分布。设事件A在每次试验中发生的概率为p，不发生的概率为q(q=1-p)，则在n次试验中，事件A恰好发生k次的概率为：

　　$$P(X=k) = C_n^k p^k q^{n-k}$$

　　其中，X表示事件A在n次试验中发生的次数。

　　求解概率问题

　　二项式定理还可以用来解决一些与概率相关的问题。例如，在抛掷一枚公平的硬币n次9znjcolz.com的情况下，求恰好出现k次正面的概率。根据二项式定理，该概率为：

　　$$P(X=k) = C_n^k \left(\frac{1}{2}\right)^k \left(\frac{1}{2}\right)^{n-k} = C_n^k \left(\frac{1}{2}\right)^n$$

　　三、二项式定理在组合数学中的应用

　　计算组合数

　　二项式定理在组合数学中的应用主要体现在计算组合数。组合数表示从n个不同元素中取出k个元素的组合方式的总数。根据二项式定理，组合数可以表示为：

　　$$C_n^k = \frac{n!}{k!(n-k)!}$$

　　其中，n!nmzhga.cn表示n的阶乘，即n! = n × (n-1) × (n-2) × ... × 1。

　　解决组合问题

　　二项式定理还可以用来解决一些与组合相关的问题。例如，在n个不同元素中，任取k个元素的排列数和组合数。根据二项式定理，排列数为：

　　$$A_n^k = \frac{n!}{(n-k)!}$$

　　组合数为：

　　$$C_n^k = \frac{n!}{k!(n-k)!}$$

　　四、总结

　　二项式定理是概率论和组合数学中的一个重要工具，它在计算概率分布、求解概率问题以及解决组合问题等方面具有广泛的应用。通过对二项式定理的深入理解和掌握，有助于我们更好地理解概率论和组合数学的内在联系，为解决实际问题提供有力支持。

特别声明：以上内容(如有图片或视频亦包括在内)为自媒体平台“网易号”用户上传并发布，本平台仅提供信息存储服务。

Notice: The content above (including the pictures and videos if any) is uploaded and posted by a user of NetEase Hao, which is a social media platform and only provides information storage services.

网址：概率论中的二项式定理与组合数学 http://c.mxgxt.com/news/view/518850

上一篇: 美动物园毒蛇失踪续：成微博明星园

下一篇: 虎牙女主播与男子逛街，水友拍下视

概率论中的二项式定理与组合数学

相关内容

随便看看

最新实时动态

热点实时动态

专题

推荐实时动态